ГОСТ Р 57700.8-2018 Численное моделирование физических процессов. Численное моделирование дозвуковых течений вязких жидкостей и газов. Верификация ПО

ГОСТ Р 57700.8-2018

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ

Численное моделирование дозвуковых течений вязких жидкостей и газов. Верификация ПО

Numerical modeling of physical processes. Numerical simulation of subsonic flows of viscous liquids and gases. Software verification

ОКС 35.020

Дата введения 2019-01-01

Предисловие

Предисловие

1 РАЗРАБОТАН Закрытым акционерным обществом "Т-Сервисы" (ЗАО "Т-Сервисы")

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 700 "Математическое моделирование и высокопроизводительные вычислительные технологии"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 6 февраля 2018 г. N 48-ст

4 ВВЕДЕН ВПЕРВЫЕ


Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)

Введение

Данный стандарт посвящен требованиям к верификации программного обеспечения компьютерного моделирования (ПО КМ), предназначенного для численного моделирования дозвуковых течений жидкости или газа. Целью верификации является подтверждение корректности программной реализации выбранных математических моделей физических процессов. Верификация других функциональных возможностей ПО КМ (ввод-вывод, пользовательский интерфейс и т.д.) рассматривается в ГОСТ Р ИСО/МЭК 12207. Основной метод верификации ПО КМ - это решение тестовых задач, покрывающих весь код ПО КМ. Рекомендуемые тесты изложены в настоящем стандарте.

В стандарте приведены аналитические решения уравнений гидромеханики, которые могут быть использованы для верификации программ при расчете дозвуковых течений невязкой и вязкой жидкостей или газа при малых дозвуковых скоростях течения.

1 Область применения

Настоящий стандарт определяет общие требования к верификации программного обеспечения компьютерного моделирования, применяемого для численного моделирования процессов, происходящих в дозвуковых течениях вязких жидкостей и газа. Дозвуковым называют течение жидкости в том случае, если ее скорость меньше скорости звука. В зависимости от рассматриваемого диапазона условий правильную картину течения можно получать в рамках моделей несжимаемой жидкости, слабосжимаемой жидкости или сжимаемой жидкости. В потоке могут присутствовать сдвиговые слои, пограничные слои и зоны рециркуляции.

Настоящий стандарт применим для верификации программного обеспечения компьютерного моделирования при проведении его валидации и сертификации.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ Р 57188 Численное моделирование физических процессов. Термины и определения

ГОСТ Р ИСО/МЭК 12207 Информационная технология. Системная и программная инженерия. Процессы жизненного цикла программных средств

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены термины по ГОСТ Р 57188.

4 Обтекание цилиндра невязким потоком

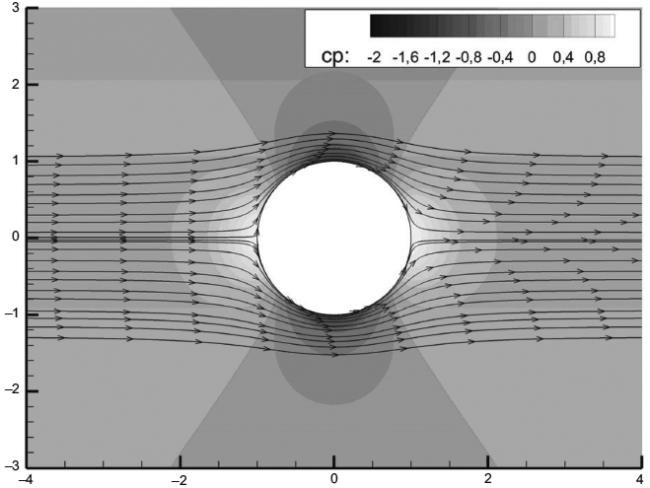
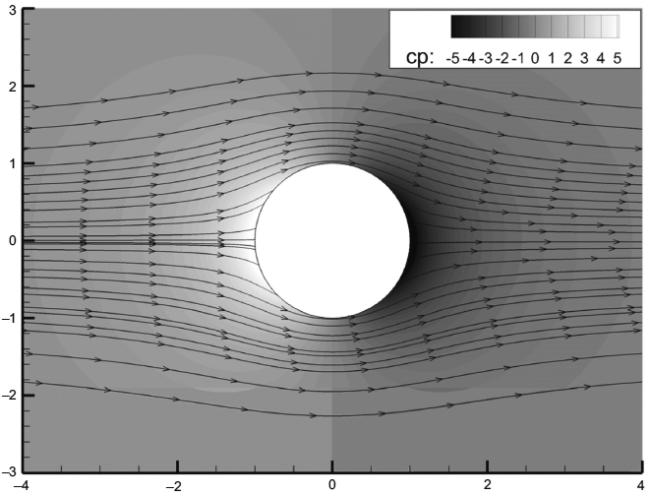
Рассматривается двумерное обтекание цилиндра потоком невязкой жидкости или невязкого газа в условиях малых дозвуковых скоростей [1] (см. рисунок 1). Цилиндр с радиусом установлен поперек потока. При предположении о потенциальном характере обтекания двумерное решение имеет вид:

- поле скоростей: 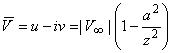, где ;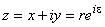

- модуль скорости на контуре цилиндра: ;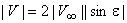

- распределение коэффициента давления по поверхности цилиндра: .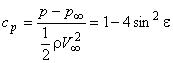

При сопоставлении результатов численного моделирования с представленным решением надо учитывать, что рассматриваемое аналитическое решение по отношению к реальным вязким течениям адекватно только на наветренной стороне цилиндра. Соответственно, если в численном моделировании используется модель невязкой жидкости, то результаты численного моделирования и аналитического решения должны совпадать во всей области течения. Если используется модель вязкой жидкости (числа Рейнольдса 10 и выше), то результаты должны соответствовать только на наветренной стороне.

Рисунок 1 - Двумерное обтекание цилиндра потоком невязкой жидкости или невязкого газа в условиях малых дозвуковых скоростей

Рисунок 1 - Двумерное обтекание цилиндра потоком невязкой жидкости или невязкого газа в условиях малых дозвуковых скоростей

5 Обтекание пластины под углом атаки

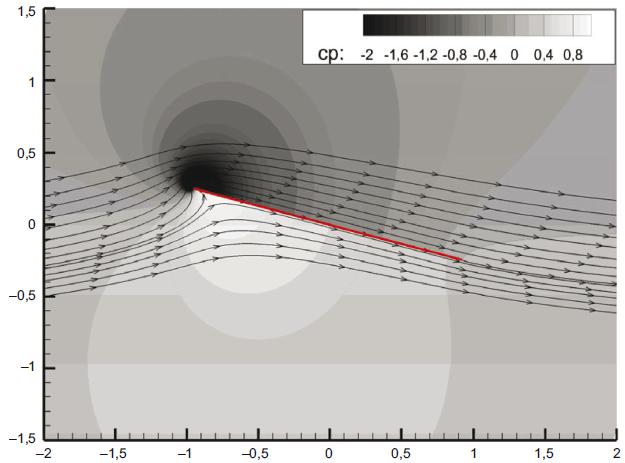
Рассматривается двумерное обтекание пластины [1] (см. рисунок 2) потоком невязкой жидкости или невязкого газа в условиях малых дозвуковых скоростей. Пластина с размером хорды 2 установлена под углом атаки . При предположении о потенциальном характере обтекания и выполнении условия Кутта - Жуковского на задней кромке крыла двумерное решение имеет вид:

- поле скоростей: 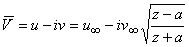, где ;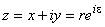

- коэффициент подъемной силы пластины: ;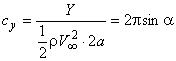

- точка положения центра давления (точка приложения подъемной силы) расположена в точке 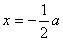или на расстоянии 1/4 длины хорды крыла от передней кромки.

При сопоставлении результатов численного моделирования с представленным решением надо учитывать, что рассматриваемое аналитическое решение справедливо при малых углах атаки (10°) в условиях безотрывного обтекания подветренной стороны. При использовании модели вязкой жидкости условие Кутта - Жуковского должно выполняться автоматически.

Рисунок 2 - Двумерное обтекание пластины

Рисунок 2 - Двумерное обтекание пластины

6 Вязкое течение около пластины, обтекаемой в продольном направлении

Рассматривается двумерное обтекание пластины длиной , установленной вдоль потока, потоком вязкой жидкости или вязкого газа в условиях малых дозвуковых скоростей [2], [3]. В рамках теории пограничного слоя известно решение о профиле скорости около пластины.

При предположении о ламинарном характере обтекания:

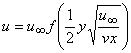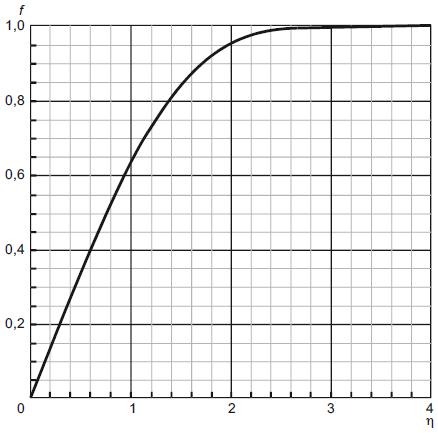
- выражение для скорости вдоль потока имеет вид: , - коэффициент кинематической вязкости. Функция , где 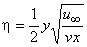, приведена в таблице 1 и на рисунке 3;

- местный коэффициент трения: , ;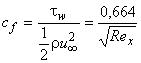

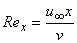- полная сила сопротивления трения пластины длиной , обтекаемой с двух сторон:

, .

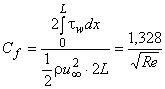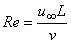Ламинарный характер течения сохраняется при числах Рейнольдса 5·10. Приведенное решение, полученное в рамках теории пограничного слоя, непременимо при малых числах Рейнольдса. Число Рейнольдса должно быть более 10(3).

Таблица 1 - Зависимость

Рисунок 3 - Зависимость "функция"("эта")

Рисунок 3 - Зависимость

7 Спутное течение за плоской пластиной

Рассматривается течение в следе за пластиной длиной , установленной вдоль потока, потоком вязкой жидкости или вязкого газа в условиях малых дозвуковых скоростей. При предположении о ламинарном характере обтекания в рамках теории пограничного слоя известно решение о профиле скорости в следе за пластиной [2].

Выражение для скорости вдоль потока имеет вид:

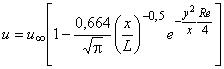, где .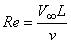

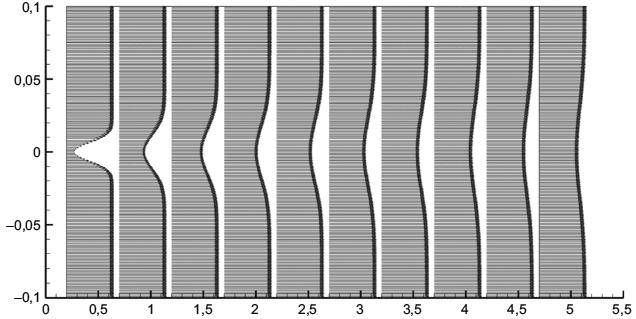
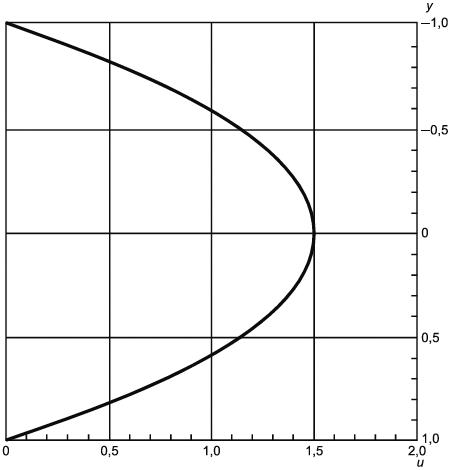
Пример профилей скорости приведен на рисунке 4.

Рисунок 4 - Пример профилей скорости

Рисунок 4 - Пример профилей скорости

8 Невязкое обтекание сферы

Рассматривается обтекание сферы радиусом потоком невязкой жидкости или невязкого газа в условиях малых дозвуковых скоростей [1]. При предположении о потенциальном характере обтекания осесимметричное решение имеет вид (см. рисунок 5):

- поле скоростей: , .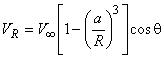

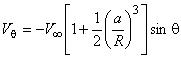Переход к компонентам скорости в цилиндрической системе координат:

, ;

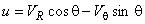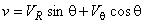- скорость на поверхности сферы: ;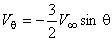

- распределение коэффициента давления по поверхности сферы:

.

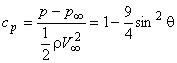При сопоставлении результатов численного моделирования с представленным решением надо учитывать, что рассматриваемое аналитическое решение по отношению к реальным вязким течениям адекватно только на наветренной стороне сферы. Соответственно, если в численном моделировании используется модель невязкой жидкости, то результаты численного моделирования и аналитического решения должны совпадать во всей области течения. Если используется модель вязкой жидкости, то результаты должны соответствовать только на наветренной стороне.

Рисунок 5 - Невязкое обтекание сферы. Осесимметричное решение при предположении о потенциальном характере обтекания

Рисунок 5 - Невязкое обтекание сферы. Осесимметричное решение при предположении о потенциальном характере обтекания

9 Вязкое обтекание сферы

Рассматривается медленное стационарное обтекание сферы (задача Стокса) радиусом потоком невязкой жидкости или невязкого газа в условиях малых дозвуковых скоростей [1], [2]. При предположении о потенциальном характере обтекания осесимметричное решение имеет вид (см. рисунок 6):

- поле скоростей:

, .

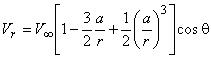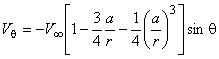Переход к компонентам скорости в цилиндрической системе координат:

, ;

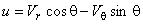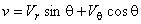- распределение давления: ;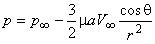

- касательная составляющая напряжения трения на поверхности сферы:

;

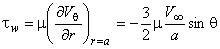- распределение коэффициента давления по поверхности сферы:

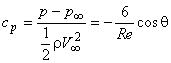, где ;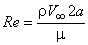

- сила сопротивления на сферу: ;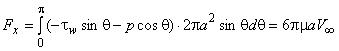

- коэффициент сопротивления сферы: .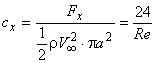

Стационарное течение при медленном обтекании сферы по Стоксу соответствует реальным течениям при очень малых числах Рейнольдса, менее чем 1.

Рисунок 6 - Вязкое обтекание сферы. Осесимметричное решение при предположении о потенциальном характере обтекания

Рисунок 6 - Вязкое обтекание сферы. Осесимметричное решение при предположении о потенциальном характере обтекания

10 Течение между вращающимися цилиндрами

Рассматривается движение жидкости или газа при малых дозвуковых скоростях между двумя коаксиальными цилиндрами, вращающимися вокруг своей оси с угловыми скоростями и , радиусы цилиндров и () [4]. При предположении симметрии течения (течение плоское, составляющая скорости по радиусу равна 0) решение имеет вид:

- составляющая скорости в окружном направлении в зависимости от радиуса :

;

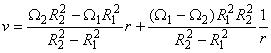- давление определяется из уравнения:

;

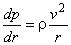- сила трения на поверхности внутреннего цилиндра:

;

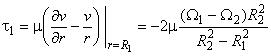- момент силы трения на внутренний цилиндр:

.

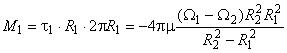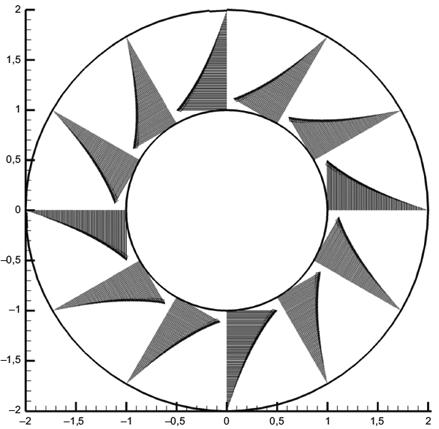
На рисунке 7 приведены профили скорости для случая, когда внешний цилиндр не вращается. С увеличением числа Рейнольдса описанное так называемое регулярное течение теряет устойчивость. Если рассматривается конфигурация цилиндров 1, 2, 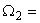0, а число Рейнольдса определяется как 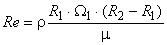, то регулярное решение сохраняется при числах Рейнольдса 80. При дальнейшем увеличении числа Рейнольдса 80 течение становится трехмерным с образованием вихрей Тейлора.

Рисунок 7 - Профили скорости для случая, когда внешний цилиндр не вращается

Рисунок 7 - Профили скорости для случая, когда внешний цилиндр не вращается

11 Течение в канале

11.1 Течение в плоском канале

Рассматривается ламинарное течение вязкой жидкости или вязкого газа при малых дозвуковых скоростях между двумя плоскостями 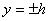[1], [2]. Решение имеет вид (см. рисунок 8):

- распределение скорости: ;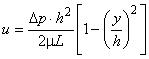

- секундный объемный расход, отнесенный к единице длины:

;

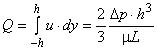- средняя скорость: ;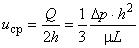

- коэффициент сопротивления: 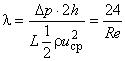, где .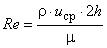

Рисунок 8 - Решение течения в плоском канале. Зависимость компоненты скорости от координаты

Рисунок 8 - Решение течения в плоском канале. Зависимость компоненты скорости от координаты

11.2 Течение в осесимметричном канале

Рассматривается ламинарное течение вязкой жидкости или вязкого газа при малых дозвуковых скоростях в круглой трубе с радиусом [1], [2]. Решение имеет вид (см. рисунок 9):

- распределение скорости: ;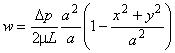

- секундный объемный расход, отнесенный к единице длины: ;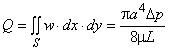

- средняя скорость: ;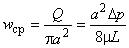

- коэффициент сопротивления: 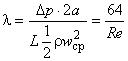, где .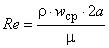

Рисунок 9 - Течение в осесимметричном канале. Зависимость компоненты скорости от координаты

Рисунок 9 - Течение в осесимметричном канале. Зависимость компоненты скорости от координаты

11.3 Течение в канале с эллиптическим сечением

Рассматривается ламинарное течение вязкой жидкости или вязкого газа при малых дозвуковых скоростях в трубе с эллиптическим сечением [1], [2]. Эллиптическое сечение задается уравнением 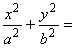1. Решение имеет вид (см. рисунок 10):

- распределение скорости: ;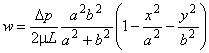

- секундный объемный расход, отнесенный к единице длины:

;

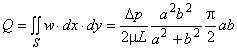- средняя скорость: ;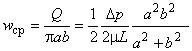

- коэффициент сопротивления: 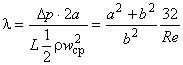, где .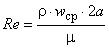

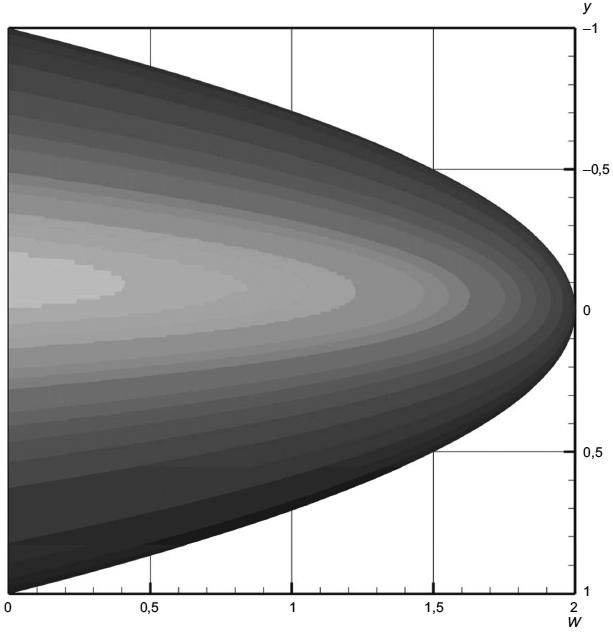
Рисунок 10 - Течение в канале с эллиптическим сечением. Решение

Рисунок 10 - Течение в канале с эллиптическим сечением. Решение

Библиография

Электронный текст документа
и сверен по:
официальное издание
М.: Стандартинформ, 2018